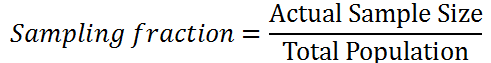Systematic Sampling
In systematic sampling (also called systematic random sampling) every Nth member of population is selected to be included in the study. It is a probability sampling method. Systematic sampling can be more suitable than simple random sampling because the former can be time-consuming.
It has been stated that “with systematic sampling, every Kth item is selected to produce a sample of size n from a population size of N”[1]. This method requires an approximated frame for a priori but not the full list.
Systematic sampling
As it is the case with any other sampling method, you will have to obtain confirmation from your dissertation supervisor about your choice of systematic sampling, total size of population, size of your sample group and the value of N sample fraction before starting collecting the primary data.
There are three types of systematic random sampling:
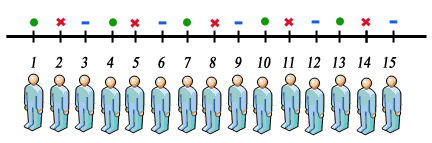
1. Systematic random sampling. In this method researcher determines sampling interval and starting from the random point uses this interval to select sample group members.
2. Linear systematic sampling. This method divides N population size into n groups, where each group consists of k Then, sampling interval k=N/n applied to form the sample group.
3. Circular systematic sampling. Population members are arranged in a circular manner and sample group members are chosen in a cyclic manner.
Application of Systematic Sampling: an Example
You can apply systematic sampling in your thesis in the following manner:
1. Label each member of the sample group with a unique identification number (ID). Accordingly, application of this method requires the knowledge of the size of total target population. You cannot use systematic sampling if you don’t know the size of the total population.
2. Calculate the sampling fraction by dividing the sample size to the total number of the population:
The sampling fraction (also called sampling interval) result is guidance for applying systematic sampling. Sampling fraction is a constant interval used to choose sample group members. For example, if your sampling fraction is equal to 1/5, you will need to choose one in every five cases; that is every fifth case from the sampling frame. In instances where calculations result in a more complicated fraction, especially for large sample sizes, you can round your population to the nearest 10 or 100.
3. The first sample has to be chosen in a random manner. It is important to select the first sample randomly to ensure probability sampling aspect of systematic sampling. In other words, if the first sample is selected from the start of the sample frame all the time, the samples between the sample fractions (samples between every fifth cases in example above) will not have a chance of being included in the sample group. Therefore, the fist case needs to be selected randomly to overcome this issue.
4. Additional members of sample group are chosen by recruiting each Nth subject (5thsubject in example above) among the population.
Let’s illustrate the application of stages above using a specific example.
Suppose your dissertation topic is “A Study into the Impact Leadership Style on Employee Motivation in ABC Company” and you have chosen semi-structured in-depth interview as primary data collection method. ABC Company has 200 operational level employees who could be potentially interviewed. You identified your sample size as 24 subjects, i.e. you will interview 24 employees.
You will have to do the following:
a) Label each employee with a unique number.
b) Calculate the sampling fraction.
Sampling fraction = (Actual Sample Size) / (Total Population) = 24/200 = 3/25.
This sampling fraction can be narrowed down to 1/8. Accordingly, every 8th member of the sampling frame needs to be selected to participate in the study.
c) Choose the first sample randomly. Suppose you randomly selected the sample #47 as the starting point for selecting samples. Accordingly, your sample group will comprise of ABC Company employees under the following numbers: #47; #55; #63; #71; #79; #87; #95; #103; #111; #119; #127; #135; #143; #151; #159; #167; #175; #183; #191; #199; #7; #15; #23; #31.
Advantages of Systematic Sampling
- When done correctly, this method will approximate the results of simple random sampling.
- Systematic sampling is cost and time efficient. The selection of a sample is very convenient. This is an important aspect of systematic sampling which makes it applicable in many situations.
- Systematic sampling is effectively suitable in collecting data from geographically disperse cases (that do not require face-to-face contact).
- Systematic sampling reduces the probability of contaminating the data
- This method eliminates the phenomenon of clustered selection
Disadvantages of Systematic Sampling
- Systematic sampling can be applied only if the complete list of population is available.
- If there are periodic patterns within the dataset, the sample will be biased.
- If study participants deduce the sampling interval, this can bias the population as non-participants will be different from study participants.
- The risk of over-representation or under-representation of particular patterns
- Greater risk of manipulations with data.
My e-book, The Ultimate Guide to Writing a Dissertation in Business Studies: a step by step approach contains a detailed, yet simple explanation of sampling methods. The e-book explains all stages of the research process starting from the selection of the research area to writing personal reflection. Important elements of dissertations such as research philosophy, research approach, research design, methods of data collection and data analysis are explained in this e-book in simple words.
John Dudovskiy
References
[1] Bajpai, N. (2010) “Business Statistics” Pearson Education India